CSCI 241 Labs: PreLab 8
Linear Regression

Linear Regression

Linear regression is the process of taking a set of points and trying to fit a line through them. As you should recall from math class, two points determine a line. When there are more than two points, most likely they won't all fall on a perfect straight line, but they may be, and often are close. For any set of points there is one line that "best" fits the data. Finding the best fit line has many applications in science and business. For example, newspapers are full of stories about global warming. Scientists are collecting a huge amount of data. Linear regression analysis should help them understand how fast the earth is warming and what the average temperature will be at some future date.

The form of the line is 

y = mx + b, where m is the slope of the line and b is the y intercept.

The formula for m is: 
     Sum(xi*yi) - n*xavg*yavg
m = ------------------------ , 
     Sum(xi2) - n*xavg2

where n is the number of points in the data set.

Since just one x and y specify just one point, we will use two arrays: one to hold the x-values and one to hold the y-values.

The formula for b is: 

b = yavg - m*xavg

Correlation

Another basic question that scientists ask is: How good is the best fit line? This is measured using a statistic called correlation, or because it is slightly easier to calculate, the square of the correlation. The square of the correlation always lies between 0 and 1. A value close to 1 means the data is fairly linear. A value close to 0 means the data is scattered about randomly.

Continuing with our global warming example, if a scientist comes up with the square of the correlation at 0.999, this means that she can predict very accurately how fast the earth is warming. If she comes up with a square of the correlation at only 0.256, the data doesn't accurately predict how fast the earth is warming.

The formula for the square of the correlation is: 

        (n*Sum(xi*yi) - Sum(xi) * Sum(yi))2
r2 = -----------------------------------------------------
        (n*Sum(xi2) - Sum(xi)2) * (n*Sum(yi2) - Sum(yi)2)

An Example

Walking through an example can help clarify the ideas and the calculations. Here is some actual data for a student who kept track of two values: X = the number of lines of code in their program, and Y = the number of hours it took to finish the program.
n X Y X2 Y2 X*Y
1 186 15.0 34596 225.0 2790
2 699 69.9 488601 4886.01 48860.1
3 132 6.5 17424 42.25 858
4 272 22.4 73984 501.76 6092.8
5 291 28.4 84681 806.56 8264.4
6 331 65.9 109561 4342.81 21812.9
7 199 19.4 39601 376.36 3860.6
8 1890 198.7 3572100 39481.69 375543
9 788 38.8 620944 1505.44 30574.4
10 1601 138.2 2563201 19099.24 221258
Total 6389 603.2 7604693 71267.12 719914.4

The first three columns represent our data. The right three columns represent calculations we do on the data.

Using the sums of X and Y we can quickly calculate the averages:

n = 10
Xavg = 6389/10 = 638.9

Yavg = 603.2/10 = 60.32

Using the sums in the table and the averages we can find all our statistics: 

       719914.4 - 10 * 638.9 * 60.32
m = ----------------------------------- = 0.094962425
          7604693 - 10 * 638.92

b = 60.32 - 0.094962425 * 638.9 = -0.351493739

Our equation becomes: 

y = 0.095 x - 0.3515

This equation takes the number of lines of code as its input and predicts how long it will take this student to finish the program. For example, if the program is 200 lines long, then 

y = 0.095 * 200 - 0.3515 = 18.64
or 18.64 hours.

The correlation squared is: 

           (10*719,914.4 - 6389*603.2)2
r2 = --------------------------------------------- = 0.9107
      (10*7604693 - 63892)*(10*71267.12 - 603.22)

r2 = 0.9107 tells us that the size of the program is a very good indicator of how long it will take the student to finish the project.

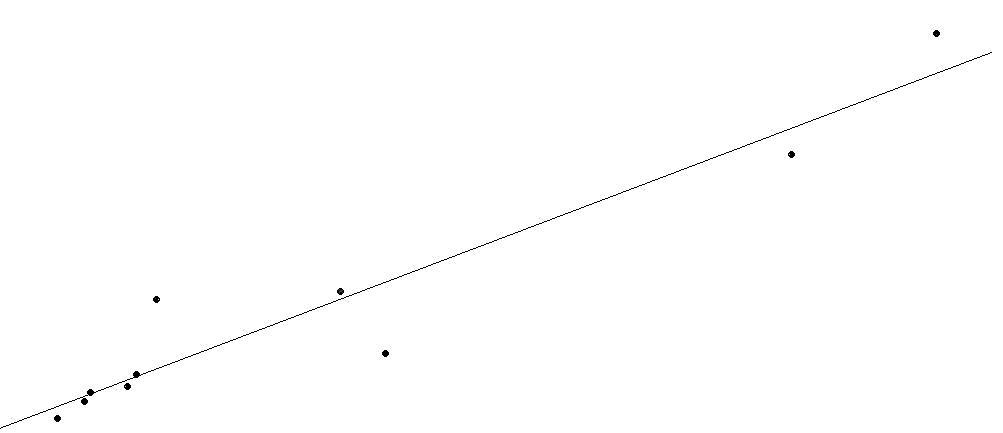
If we graph the data points and the line, we see that the line goes right through the "middle" of the collection of points.

Linear regression can be used for all sort of predictions.

Finally, many real world phenomena are do not follow linear trends. For example, the earth's population in recent history has been growing exponentially, not linearly. There are other mathematical modelling techniques available to help make these predictions. In reality, the math to match a exponential curve to data is very similar to what we have done here.